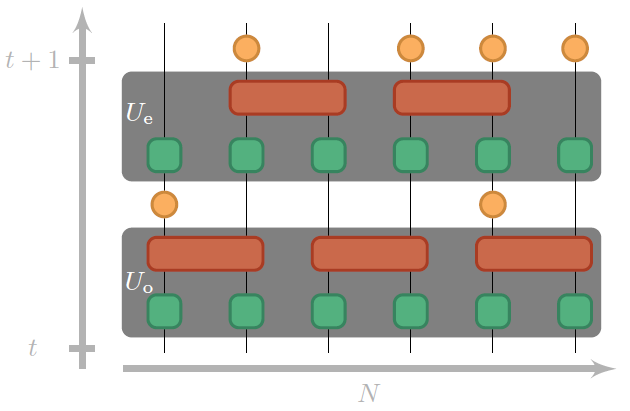
In this theoretical proposal, we describe a hybrid circuit where coherent time evolution is interrupted by sparse projective measurements. A measurement-driven phase transition between volume-law and area-law entanglement is predicted at a specific rate of measurement. Proof-of-principle experiments can be performed in modern trapped ion quantum information processors.

Abstract: The rise of programmable quantum devices has motivated the exploration of circuit models which could realize novel physics. A promising candidate is a class of hybrid circuits, where entangling unitary dynamics compete with disentangling measurements. Novel phase transitions between different entanglement regimes have been identified in their dynamical states, with universal properties hinting at unexplored critical phenomena. Trapped ion hardware is a leading contender for the experimental realization of such physics, which requires not only traditional two-qubit entangling gates, but a constant rate of local measurements accurately addressed throughout the circuit. Recent progress in engineering high-precision optical addressing of individual ions makes preparing a constant rate of measurements throughout a unitary circuit feasible. Using tensor network simulations, we show that the resulting class of hybrid circuits, prepared with native gates, exhibits a volume-law to area-law transition in the entanglement entropy. This displays universal hallmarks of a measurement-induced phase transition. Our simulations are able to characterize the critical exponents using circuit sizes with tens of qubits and thousands of gates. We argue that this transition should be robust against additional sources of experimental noise expected in modern trapped ion hardware, and will rather be limited by statistical requirements on post selection. Our work highlights the powerful role that tensor network simulations can play in advancing the theoretical and experimental frontiers of critical phenomena.